Logic
I. Some basic concepts:
A. Logical and View
video
Written
notes to summarize the video:
"Logical
and" is a little
different from ordinary English "and" because "logical and" can only
join sentences. So
you get
something like: <Short sentence A> and <short
sentence B> and
... <short sentence Z>. For the whole
long
sentence to be true, each
part of it must be true. We would not accept as true
a
statement such as,
"George
Washington was a Russian,
and he was the first president of the United States," even though the
second
part of
the long sentence is true
B. Logical or (non-exclusive
or) View
video
Written
notes to summarize the video:
"Logical
or" is sometimes called "non-exclusive or" because one part of it being
correct does not exclude
the
second part of it from being
correct. We often use "or" sentences when we have
made a
partial determination
but can't
settle on a single
answer, e.g., "She is a medical doctor, or she is an attorney at law."
Possibly she is both.
C. The symbols used to indicate "and"
and "or" sentences View
video
Written
notes to summarize the video:
Logic books can use
different symbols for "and," "or," and other logical connectives.
We will use the
ampersand
(&) because
it is a way of writing the Latin word for "and" (et) as the letters "e"
and "t" joined together.
(Some
books use "∧.")
Most
logic books use "∨" for
"or." That is because the Latin word for "non-exclusive or"
is
"vel."
People
ordinarily chose the first
letter of one key word in a sentence to represent that sentence in
logical form. So for
"Minnows
are small and whales
are large," we might write: M & W. For "She
is a singer
or she is a pianist,"
we
might
write: "S ∨ P."
D. The truth table for and sentences. View
video
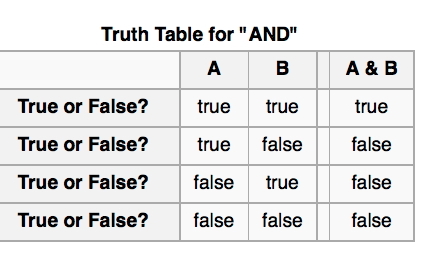
Written
notes to summarize the truth table for and sentences.
This
truth table is very straightforward. It shows that "logical and" sentences are
only true when both shorter, component,
sentences
are true.
E. The truth table for or sentences.View video
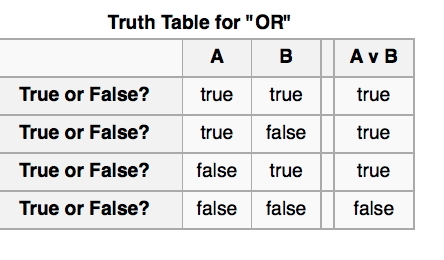
Written
notes to summarize the truth table for or sentences:
This truth tables is also pretty
straightforward. They just look at two simple sentences at a
time, noting whether
each
simple sentence is true or
false, and then set down a determination as to whether we would call
their logical
"or"
combination true or false.
F. If...Then...
sentences and their truth tables View
video
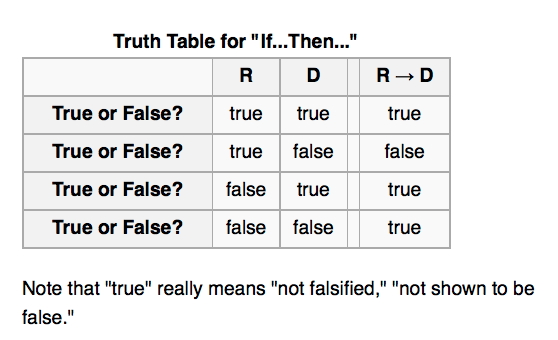
Written
notes to summarize the truth table for "if... then..." sentences:
This
truth table often causes trouble if ridiculous examples are provided
students. Professor Maylon Hepp gives a
very
useful example in his book Thinking
things through: An introduction to logic: "If I
give you a penny, then I
will give
you a dollar."
Under what circumstances would we call Professor Hepp a liar?
Only if he gives us a
penny and
then refuses to give us
a dollar. If he just gives us a dollar, we have no right to
complain. He never said
he would
give us a dollar only if
he first gave us a penny. He's just being generous. If he
gives us nothing, he's not
been
demonstrated to be a liar
either. He never promised to give us anything. He just promised or
predicted what
he would
do providing he first gave us a penny.
G. .....If
and only if..... sentences and their truth tables
View First Video
View Second Video
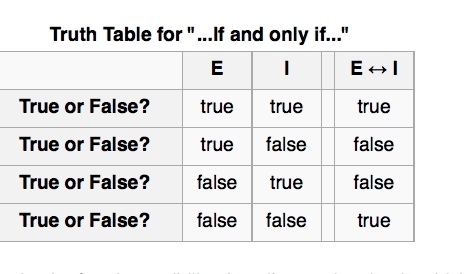
Written
notes to summarize the truth table for "if... then..." sentences:
If I say,
"I will give you a
dollar if and only if I give you a penny," then I am not telling the
truth if I only give you
a penny
or if I only give you a
dollar. If I give you both, it is clear that I was telling the truth.
If I give you nothing
then I
have not been demonstrated to be a liar.
H. Overview of all truth tables examined
so far.View
video
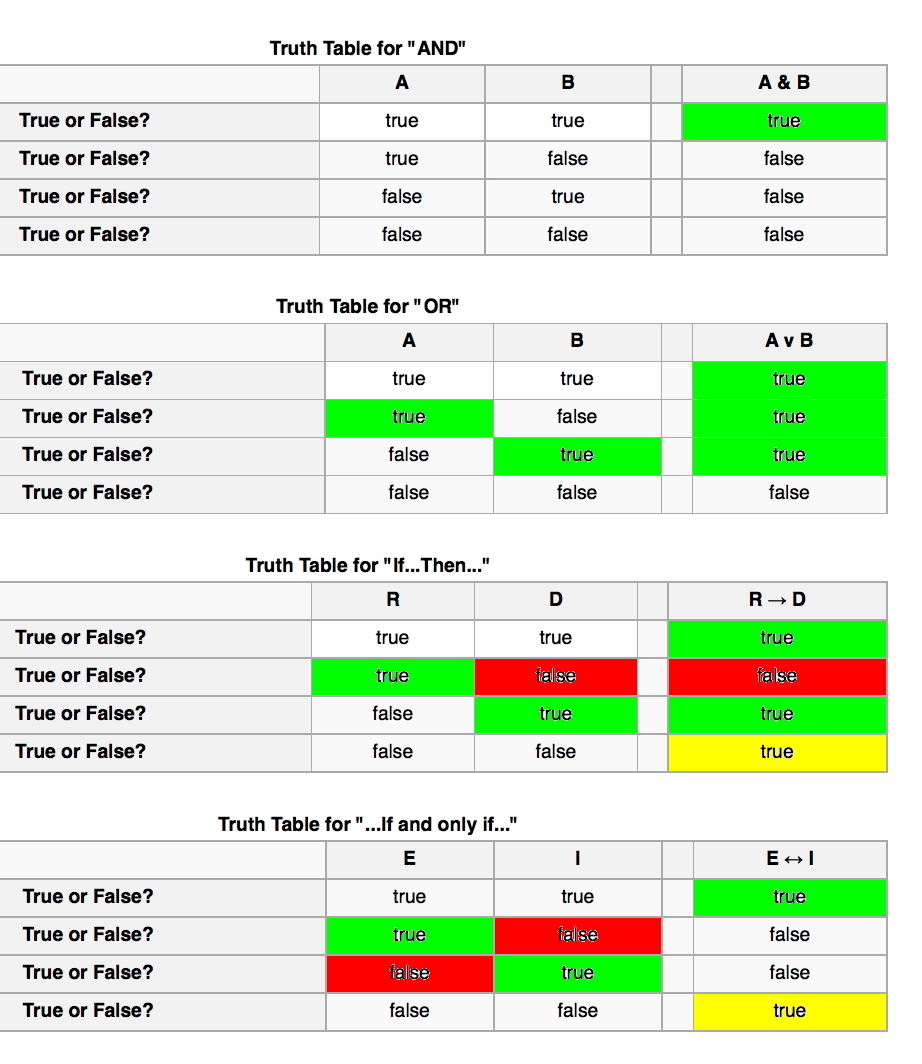
Written
notes to summarize the truth table for all sentences
covered so far:
Note that the crucial thing in the "and"
table is to
have all the short sentences (A, B,...) be true.
Note that the crucial thing in the "or"
table is to
have at least one of the short sentences be true.
Note that the crucial thing in the
"if... then..."
table is the case where the "if" part is true, but the "then"
part
is not true. Also note that if
neither R or D
is true, then nothing relevant has happened, so the "if-then"
statement
has not been tested. In that case it is counted as being
true. We would never know for sure
whether the logical implication was true
unless a
case occurred in which R was true.
Note that the crucial thing for the "if
and only if"
table are the cases where one of the shorter sentences is
true and its counterpart is false. When
both are
false, the whole thing is counted
as being true because its
truth has
not been challenged.




